Quadratic Formula
Table of Contents
$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$
Where
- \(x\) is the solution to the quadratic equation \(ax^2 + bx + c = 0\),
- \(a\) is the coefficient of the \(x^2\) term,
- \(b\) is the coefficient of the \(x\) term, and
- \(c\) is the constant term
Sources #
Example #
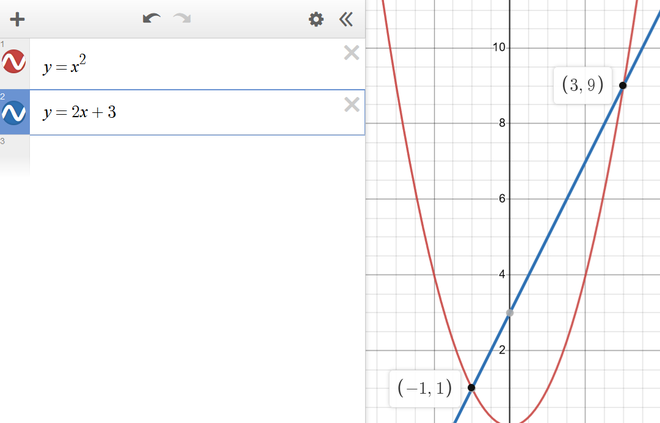
Find the intersection points of the parabola \(y = x^2\) and the line \(y = 2x + 3\).
We know that these two will intersect when \(x^2 = 2x + 3\). We can solve this quadratic equation using the quadratic formula.
First, we rearrange to get it into the correct form: \(x^2 - 2x - 3 = 0\). Then, we plug in the coefficients into the quadratic formula, with a = 1, b = -2, and c = -3.
$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \Longrightarrow x = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(1)(-3)}}{2(1)} $$
$$\Longrightarrow x = \frac{2 \pm \sqrt{4 + 12}}{2} \Longrightarrow x = \frac{2 \pm 4}{2} \Longrightarrow x = 3, -1$$
Plugging these x values into either of the original equations gives us the y values of the intersection points.
The final answer is \((3, 9)\) and \((-1, 1)\), which we can verify on a graph: